Update: With changes introduced in January 2013 you only need 1GB – live demo!

In one of my last blog posts I wrote about memory efficient ways of coding Java. My conclusion was not a bright one for Java: “This time the simplicity of C++ easily beats Java, because in Java you need to operate on bits and bytes”. But I am still convinced that in nearly every other area Java is a good choice. Just some guys need to implement the dirty parts of memory efficient data structures and provide a nice API for the rest of the world. That’s what I had in mind with

GraphHopper

GraphHopper does not attack memory efficient data structures like Trove4j etc. Instead it’ll focus on spatial indices, routing algorithms and other “geo-graph” experiments. A road network can already be stored and you can execute Dijkstra, bidirectional Dijkstra, A* etc on it.

Months ago I took the opportunity and tried to import the full road network of Germany via OSM. It failed. I couldn’t make it working in the first days due to massive RAM usage of HashMaps for around 100 mio data points (only 33 mio are associated to roads though). Even using only trove4j brought no success. When using Neo4J the import worked, but it was very slow and when executing algorithms the memory consumption was too high when too many nodes where requested (long paths).

Then after days I created a memory mapped graph implementation in GraphHopper and it worked too. But the implementation is a bit tricky to understand, not thread safe (even not for two reading threads yet), slower compared to a pure in-memory solution. But even more important: the speed was not very predictable and very ugly to debug if off-heap memory got rare.

I’ve now created a ‘safe’ in-memory graph, which saves the data after import and reads once before it starts. At the moment this is read-thread-safe only, as full thread safety would be too slow and is not necessary (yet).

Now performance wise on this big network, well … I won’t talk about the speed of a normal Dijkstra, give me some more time to improve the speed up technics. For a smaller network you can see below that even for this simplistic approach (no edge-contraction or edge-reduction at all) the query time is under 150ms and will be under 100ms for bidirectional A* (w/o approximation!), I guess.

In order to perform realistic route queries on a road network we would like to satisfy two use cases:

1. Searching addresses (cities, streets etc)
2. Clicking directly on the map to create a route query

The first one is simple to solve and it is very unlikely to avoid tons of additional RAM. But we can solve it very easy with ElasticSearch or Lucene: just associate the cities, streets etc to the node ids of the graph.

The second use case requires more thinking because we want it memory efficient. A normal quad-tree is not a good choice as it requires too many references. Even for a few million data points it requires several dozens of MB in addition to the graph! E.g. 80MB for only 4 mio nodes.

The solution is to use a raster over the area – which can be a simple array addressed by spatial keys. And per quadrant (aka tile) we store one array index of the graph as entry point. (In fact this is a quad-tree of depth one!) Then when a click on the map happened, we can calculate the spatial key from this point (A), then get the entry point from the array and traverse the graph to get the point in the graph which is the closest one to point A. Here is an implementation, where only one problem remains (which is solved in the new index).

Unfair Comparison

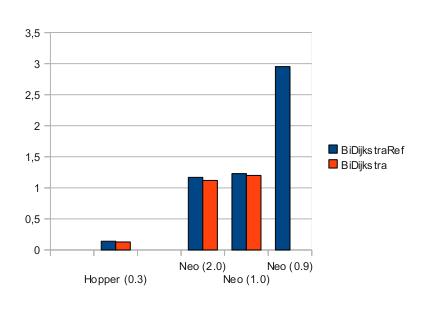
In the last days, just for the sake of fun, I took Neo4J and ran my bidirectional Dijkstra with a small data set – unterfranken (1 mio nodes). GraphHopper is around 8 times faster and uses 5 times less RAM:

The lower the better – it is the mean time in seconds per run on this road network where two of the algorithms (BiDijkstraRef, BiDijkstra) are used. The number in brackets is the actually used memory in GB for the JVM. The lowest possible memory for GraphHopper was around 160MB, but only for the more memory friendly version (BiDikstra).

For all Neo4J-Bashers: this is not a fair comparison as GraphHopper is highly specialized and will only be usable for 2D networks (roads, public transport) and it is also does not have transaction support etc. as pointed out by Michael:

But we can learn that sometimes it is really worth the effort to create a specialized solution. The right tools for the right job.

Conclusion

Although it is not easy to create memory efficient solutions in Java, with GraphHopper it is possible to import (2.5GB) and use (1.5GB) a road network of the size of Germany on a normal sized machine. This makes it possible to process even large road networks on one machine and e.g. lets you run algorithms on even a single, small Amazon instance. If you reduce memory usage of your (routing) application you are also very likely to avoid garbage collection tuning.

There is still a lot room to optimize memory usage and especially speed, because there is a lot of research about road networks! You’re invited to fork & contribute!

In Java land there are at least two quadtree implementations which are not yet optimal, so I though I’ll post some possibilities to tune them. Some of those possibilities are already implemented in my GraphHopper project.

Quadtree

What is a quadtree? Wikipedia says: “A quadtree is a tree data structure in which each internal node has exactly four children.” And then you need some leaf nodes to actually store some data – e.g. points and associated values.

A quadtree is often used for fast neighbor searches of spatial data like points or lines. And a quadtree with points could work like the following: fill up a leaf node until its full (e.g. 8 entries), then create a branch node with 4 pointers (north-west, north-east, south-west, south-east) and decide where the leaf node entries should go depending of its location, in this process it could be necessary to create new branch nodes if all entries are too much clustered.

Now a simple neighbor search can be implemented recursively. Starting from the root node:

• If the current node is a leaf node check if the point is in the search area. If that is the case add it to the results
• If it is branch node check if one of the 4 sub-areas intersects with the search area. If a sub-node intersects then use that as current node and call this method recursively.

Trick 1 – Normalize the Distance

Searches are normally done with a point and a radius. To check if the current area of the quadrant intersects with the search area you need to calculate the distance using the Haversine formula. But you don’t need to calculate it every time in its entire complexity. E.g. you can avoid the following calculation:

R * 2 * Math.asin(Math.sqrt(a));

This is ok, if you have already normalized the radius of the search area via:

double tmp = Math.sin(dist / 2 / R);
return tmp * tmp;

Trick 2 – Use Smart Intersect Methods

The intersect method should fail fast. E.g. when you use again a circle as search area you should calculate only once the bounding box and check intersection of this with the quadrant area before applying the heavy intersect calculation with the Haversine formula:

public boolean intersect(BBox b) {
    // test top intersect
    if (lat > b.maxLat) {
        if (lon < b.minLon)
            return normDist(b.maxLat, b.minLon)  b.maxLon)
            return normDist(b.maxLat, b.maxLon)  0;
    }

    // test bottom intersect
    if (lat < b.minLat) {
        if (lon < b.minLon)
            return normDist(b.minLat, b.minLon)  b.maxLon)
            return normDist(b.minLat, b.maxLon)  0;
    }

    // test middle intersect
    if (lon < b.minLon)         return bbox.maxLon - b.minLon > 0;
    if (lon > b.maxLon)
        return b.maxLon - bbox.minLon > 0;
    return true;
}

Also be very sure you defined your bounding box properly once and for all. I’m using: minLon, maxLon followed by minLat which is south(!) and maxLat. Equally to EX_GeographicBoundingBox in the ISO 19115 standard see this discussion.

Trick 3 – Use Contains() and not only Intersect()

Now a less obvious trick. You could completely avoid intersect calls of quadrant areas which lay entirely in the search area. For this it is necessary to calculate fast if the search area fully contains the quadrant area or not. E.g. the method for a boudning box containing another bounding box would be:

class BBox {
  public boolean contains(BBox b) {
    return maxLat >= b.maxLat && minLat = b.maxLon && minLon   }
  ...
}

Similar for BBox.contains(Circle), Circle.contains(BBox) and Circle.contains(Circle).

Trick 4 – Sort In Time and not just Adding

Normally you want only 10 or less nearest neighbors and not all neighbours in a fixed distance. Especially for search engines like Lucene this should be favoured. For that you should use a priority queue to handle the ordering of the result. But not only of the leaf nodes – also when deciding which branch node should be processed next! See the paper Ranking in spatial databases for more information, where also a method for incremental neighbor search is described. This would make paging through the results very efficient.

Trick 5 – Use Branch Nodes with more than Four Children

Instead of branch nodes with 4 children you could use a less memory efficient but faster arrangement: use branch nodes with 16 child nodes. Or you could even decide on demand which branch node you should use – this can lead to partially big branch arrays where the quadtree is complete – making searching very efficient as then the sub-quadtree is a linear quadtree (see below).

Tricks for linear QuadTrees

Trick 6 – Avoid costly intersect methods

This only applies if you quadtree is a linear one ie. one where you can access the values by spatial keys (aka locational code). You’ll need to compute the spatial key of all four corners of your search area bounding box. Than compute the common bit-prefix of the points and start with that bit key instead from zero to traverse the quadtree. More details are available in the paper Speeding Up Construction of Quadtrees for Spatial Indexing  p.12.

Trick 7 – Bulk processing for linear Quadtrees

If you know that a quadrant is completely contained in a search area you can not only avoid further intersection calls, but also you can completely avoid branching and loop from quadrants bottom-left point to top-right. E.g. your are at key=1011 and you know the current quadrant node is contained in the search area. Then you can loop from the index “1011 000000..” to “1011 111111..”

Trick 8 – Store some Bits from the Point in Branch Nodes

For linear quadtrees you already encoded the point into spatial keys. Now you can use a radix tree to store the data memory efficient: some bits of the spatial key can be stored directly in the branch nodes. I’ve create also a different approach of a memory efficient spatial storage but as it turns out it is not that easy to handle when you need neighbor searches.

Conclusion

As you can see a lot time can go into tuning a quadtree. But at least the first tricks I mentioned should be used as they are easy and fast to apply and will make your quadtree significant faster.

When you are operating on geographical data you can use latitude and longitude to specify a location somewhere on earth. To look up some associated information like we do in GraphHopper for the next street or if you want to do neighborhood searches you could create R-trees, quad-trees or similar spatial data structures to make them efficient. Some people are using Geohashes instead because then the neighborhood searches are relative easy to implement with simple database queries.

In some cases you’ll find binary representations of Geohashes – I named them spatial keys – in the literature I found a similar representation named locational code (Gargantini 1982) or QuadTiles at OpenStreetMap. A spatial key works like a Geohash but for the implementation a binary representation instead of one with characters is chosen:

At the first level (e.g. assume world boundaries) for the latitude we have to decide whether the point is at the northern (1) or southern (0) hemisphere. Then for the longitude we need to know wether it is in the west (0) or in the east (1) of the prime meridian resulting in 11 for the image below. Then for the next level we “step into” smaller boundaries (lat=0..90°,lon=0..+180°) and we do the same categorization resulting in a spatial key of 4 bits: 11 10

The encoding works in Java as follows:

long hash = 0;
double minLat = minLatI;
double maxLat = maxLatI;
double minLon = minLonI;
double maxLon = maxLonI;
int i = 0;
while (true) {
    if (minLat  midLat) {
            hash |= 1;
            minLat = midLat;
        } else
            maxLat = midLat;
    }

    hash <<= 1;
    if (minLon  midLon) {
            hash |= 1;
            minLon = midLon;
        } else
            maxLon = midLon;
    }

    i++;
    if (i < iterations)
        hash <<= 1;
    else
        break;
}
return hash;

When we have calculated 25 levels (50 bits) we are in the same range of float precision. The float precision is approx. 1m=40000km/2^25 assuming that for a lat,lon-float representation we use 3 digits before the comma and 5 digits after. Then a difference of 0.00001 (lat2-lat1) means 1m which can be easily calculated using the Haversine formula. So, with spatial keys we can either safe around 14 bits per point or we are a bit more precise for the same memory usage than using 2 floats.

I choose the definition Lat, Lon as it is more common for a spatial point, although it is against the mathematic point x,y.

Now that we have defined the spatial key we see that it has the same properties as a Geohash – e.g. reducing the length (“removing some bits on the right”) results in a broader matching region.

Additionally the order of the quadrants could be chosen differently – instead of the Z-curve (also known as Morton Code) you could use the Hilbert Curve:

But as you can see, this would make the implementation a bit more complicated and e.g. the orientation of the “U” order depends on previous levels –  but the neighborhood searches would be more efficient – this is also explained a bit in the paper Speeding Up Construction of Quadtrees for Spatial Indexing  p.8.

I decided to avoid that optimization. Let me know if you have some working code of SpatialKeyAlgo for it 🙂 ! It should be noted that there are other space filling curves like the ones from Peano or Sierpinsky.

One problem

while implementing this was to get the same point out of decode(encode(point)) again. The encoding/decoding schema needs to be “nearly bijective” – i.e. it should avoid rounding problems as good as possible. To illustrate where I got a problem assume that the point P (e.g. see the image above) is encoded to 1110 – so we already lost precision, when our point is now at the bottom left of the quadrant 1110. Now if we decode it back we loose again some precision due to normal double rounding errors. If we would encode that point again it could end up as 1001 – the point moved one quadrant to the right and one to the bottom! To avoid that, you need to define position of the point at the center of the quadrant while decoding. I implemented this simply by adding half of the quadrant width to the latitude and longitude. This makes the encoding/decoding stable even if there are minor rounding issues while decoding.

A nice property of the spatial key

is that one bounding box e.g. for the starting bits at level 6:

110011

goes from the bottom left point

110011 0000..

to the top-right point

110011 1111..

making it easy to request e.g. the surrounding bounding boxes of a point for every level.

Conclusion

As we have seen the spatial key is just a different representation of a Geohash with the same properties but uses a lot less memory. The next time you index Geohashes in your DB use a long value instead of a lengthy string.

In the next post you will learn how we can implement a memory efficient spatial data structure with the help of spatial keys. If you want to look at a normal quadtree implemented with spatial keys you can take a look right now at my GraphHopper project. With this quadtree neighborhood searches are approx. twice times slower than one with values for latitude and longitude due to the necessary encoding/decoding. Have a look into the performance comparison project.